Lous Blog
PID 控制器
03 Jun 2019PID控制器
无模型控制器,不需预先知道系统的传递函数就可以使用。
神奇的是PID控制器在绝大多数工程中可可用的,我们只需要调节PID参数即可获取到一个不错的控制效果。
连续PID控制器
\[u(t)=K_pe(t)+K_i\int_0^te(\tau)d\tau+K_d\frac{d}{dt}e(t)\]$u(t)$ 为控制器输出 $e(t)$ 为设定值(Set Point)和测量值(Process Value)
对上式做拉式变换,可以得到PID控制器的传递函数
\[G(s)=K_p+\frac{K_i}{s}+K_ds=\frac{K_ds^2+K_ps+K_i}{s}\]使用Octave分析传递函数
kp=0.7;
ki=0.03;
kd=0.01;
figure
Gs=tf([kd kp ki],[1]);
bode(Gs);
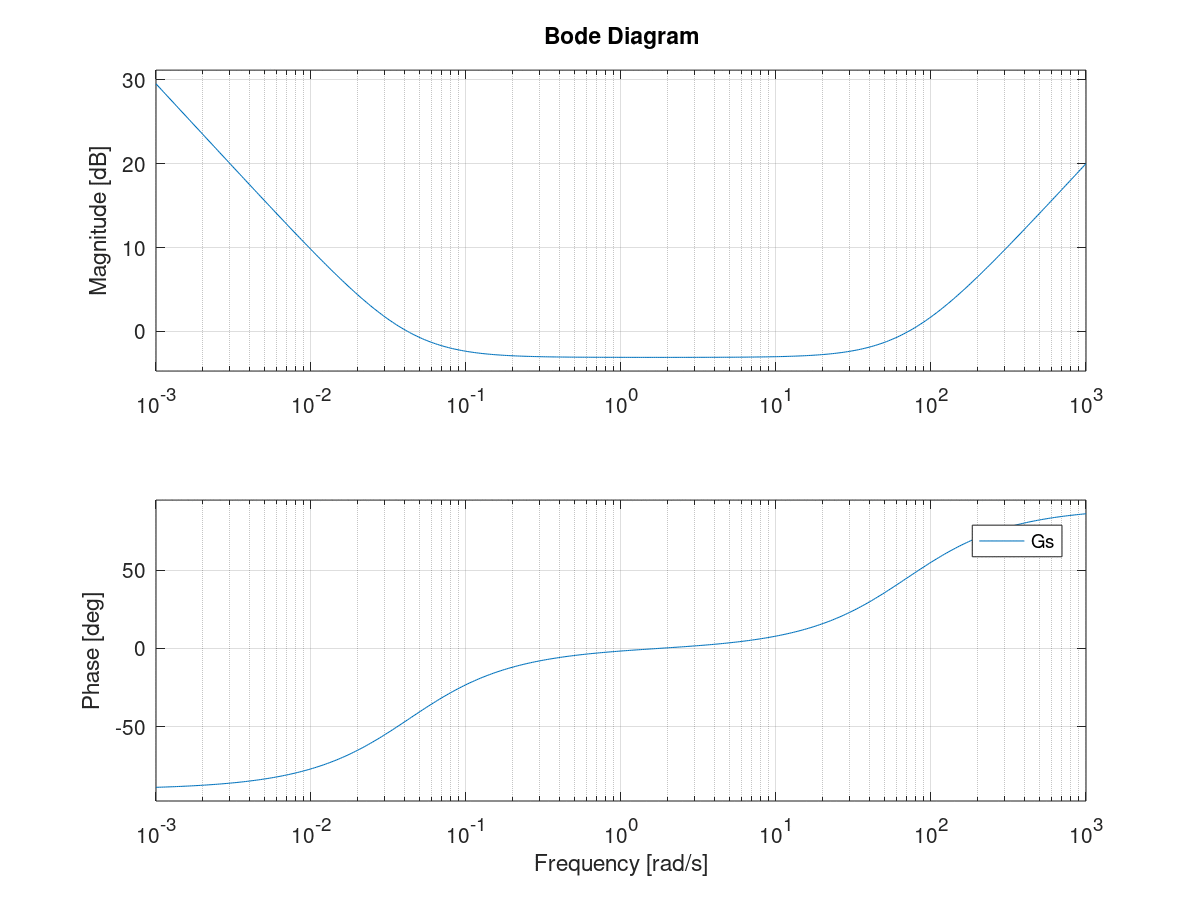
把$K_p$提取出来,可以写成标准PID形式
\[u(t)=K_p(e(t)+\frac{1}{T_i}\int_0^te(\tau)d\tau+T_d\frac{d}{dt}e(t))\]$T_i$ 积分时间 $T_d$ 微分时间
因为标准形式的PID表达式各项系数都有着具体的物理含义,所以工程上一般使用标准形式的PID表达式。
若受控系统的传递函数为$H(s)$,则整个闭环回路的传递函数为$G(s)H(s)$。
以下内容为个人理解与疑问,需后续进一步研究确认。
理解: 因为$H(s)$与受控系统的物理特性有关,认为是不会发生变化的。只需调节PID参数使$G(s)H(s)$的传输特性稳定即可。这也是为什么我们不需要知道受控系统的传递函数,仅靠一个调节过PID参数的控制器即可得到一个表现不错的闭环控制回路。 个人疑问: 假如我们给定一个初始的PID参数,仅含有比例系数。 在整个闭环回路不发散的情况下,测得闭环回路的传递函数,是否直接能够获取到$H(s)$? 如果我们计算出了$H(s)$,是否能够直接求得使得系统稳定的$G(s)$? 根据$G(s)$计算出积分和微分系数? 是不是就意味着能够自动标定PID系数了?
离散PID控制器
C语言下的伪代码
double previous_error=0.0;
double error=0.0;
//参数随机给定,无意义
double kp=0.7;
double ki=0.03;
double kd=0.01;
double setpoint=0.0;
double measured_value=0.0;
double integral,derivative,output;
double dt=1;
for(;;)
{
//获取测量系统值,可滤波
error = setpoint - measured_value;
integral += error*dt;
derivative = (error - previous_error)/dt;
output = kp*error + ki*integral + kd*derivative;
//对执行器开始操作
previous_error = error;
}
坊间流传的PID调节口诀
参数整定找最佳,从小到大顺序查. 先是比例后积分,最后再把微分加. 曲线振荡很频繁,比例度盘要放大. 曲线漂浮绕大湾,比例度盘往小扳. 曲线偏离回复慢,积分时间往下降. 曲线波动周期长,积分时间再加长. 曲线振荡频率快,先把微分降下来. 动差大来波动慢,微分时间应加长. 理想曲线两个波,前高后低四比一. 一看二调多分析,调节质量不会低.