Lous Blog
坐标系及其转换
20 Jun 2019在进行姿态估计过程中,我们需要进行坐标系转化。
图像识别定位过程,也会有相机坐标系和世界坐标系之间的转化。
三维直角坐标系转化
欧拉角 转换矩阵 旋转向量 四元数
旋转向量和四元数计算相对简单些。
欧拉角
真是哪里都离不开这个男人……
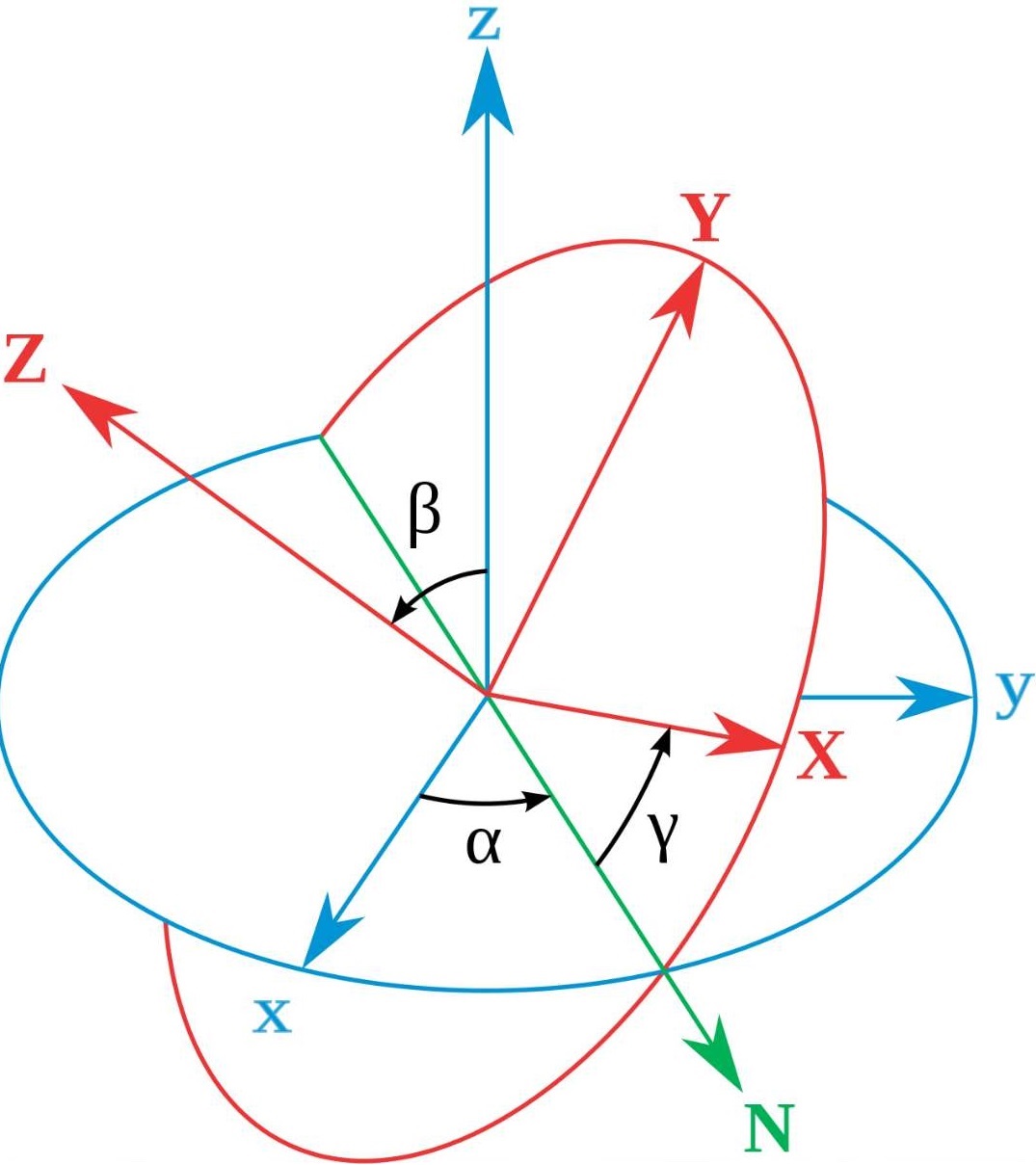
旋转矩阵表示
绕 $X$、$Y$ 或 $Z$ 单个轴旋转 $θ$ (右手螺旋)
\[\begin{bmatrix}x' \\ y' \\ z'\end{bmatrix} = R * \begin{bmatrix}x \\ y \\ z\end{bmatrix}\]其中 $R$ 就是三阶的旋转矩阵。
仅绕坐标轴的旋转矩阵可表示为
\[R_X=\begin{bmatrix} 1&0&0\\ 0&cos\theta&-sin\theta\\ 0&sin\theta&cos\theta \end{bmatrix}\] \[R_Y=\begin{bmatrix} cos\theta&0&sin\theta\\ 0&1&0\\ -sin\theta&0&cos\theta \end{bmatrix}\] \[R_Z=\begin{bmatrix} cos\theta&-sin\theta&0\\ sin\theta&cos\theta&0\\ 0&0&1 \end{bmatrix}\]任意一个旋转都可以由三个旋转组合得到。
\[\mathcal{M}(\hat{\mathbf{v}},\theta) = \begin{bmatrix} \cos \theta + (1 - \cos \theta) x^2 & (1 - \cos \theta) x y - (\sin \theta) z & (1 - \cos \theta) x z + (\sin \theta) y \\ (1 - \cos \theta) y x + (\sin \theta) z & \cos \theta + (1 - \cos \theta) y^2 & (1 - \cos \theta) y z - (\sin \theta) x \\ (1 - \cos \theta) z x - (\sin \theta) y & (1 - \cos \theta) z y + (\sin \theta) x & \cos \theta + (1 - \cos \theta) z^2 \end{bmatrix}\]通过旋转矩阵不能直观地看出旋转的方向和角度,直接能到角度算我输。
生成元表达(没看懂……)
\[\mathcal{M}(\hat{\mathbf{v}},\theta) = \exp\left( \begin{bmatrix} 0 & -z\theta & y\theta \\ z\theta & 0 & -x\theta \\ -y\theta & x\theta & 0 \\ \end{bmatrix}\right)\]旋转变换本身只有3个自由度,但旋转矩阵有9个元素,因此旋转矩阵中的元素不是相互独立的,这在非线性优化中会带来问题。
旋转向量表示
罗德里格旋转公式 Rodrigues’ rotation formula
设$\mathbf{v}$是一个三维空间向量,$\mathbf{k}$是旋转轴的单位向量,则$\mathbf{v}$在右手螺旋定则意义下绕旋转轴k旋转角度$\theta$得到的向量可以由三个不共面的向量$\mathbf{v}$, $\mathbf{k}$和$\mathbf{k} \times \mathbf{v}$构成的标架表示。
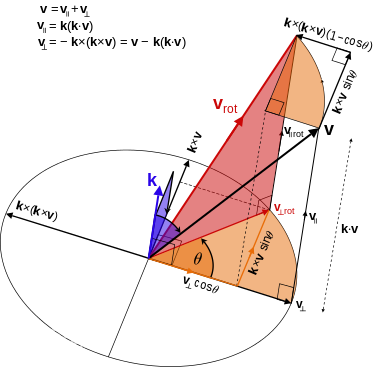
设旋转向量的单位向量为 $r$,模为 $\theta$。三维点(或者说三维向量)$p$ 在旋转向量 $r$ 的作用下变换至 $p’$,则:
\[p'=\cos\theta\cdot p+(1-\cos\theta)(p\cdot r)r+\sin\theta\cdot r \times p\]旋转向量和旋转矩阵之间的转换关系
设旋转向量的单位向量 $r=[r_x\ r_y\ r_z]^T$,旋转角度为 $θ$,对应的旋转矩阵为 $R$,则 $r$ 到 $R$ 的转换是:
\[R = \cos\theta I+(1- \cos\theta) r r^T+\sin\theta \begin{bmatrix} 0&-r_z&r_y\\ r_z&0&-r_x\\ -r_y&r_x&0 \end{bmatrix}\]其中 $I$ 是三阶单位矩阵。反过来 $R$ 到 $r$ 的转换则可以利用等式:
\[\frac{R-R^T}{2}=\sin\theta \begin{bmatrix} 0&-r_z&r_y\\ r_z&0&-r_x\\ -r_y&r_x&0 \end{bmatrix}\]四元数表示
\[q = q_0 + q_1 i + q_2 j + q_3 k\]其中
\[\begin{array}{l} {i^2} = {j^2} = {k^2} = - 1\\ ij = k,ji = - k\\ jk = i,kj = - i\\ ki = j,ik = - j \end{array}\]绕单位向量$\mathbf{n}=\left[ n_x, n_y, n_z \right]^T$进行了角度为θ的旋转,那么这个旋转的四元数形式为:
\[q = \left[ \cos \frac{\theta}{2}, n_x \sin \frac{\theta}{2}, n_y \sin \frac{\theta}{2}, n_z \sin \frac{\theta}{2}\right]^T\]根据四元数$q$我们也可以知道其旋转角和旋转轴
\[q = q_0 + q_1 i + q_2 j + q_3 k\] \[\theta = 2\arccos{ q_0 }\] \[[ n_x , n_y , n_z ]^T = [q_1,q_2,q_3]^T \sin \frac{\theta}{2}\]把三维空间点$[x,y,z]$用一个虚四元数$\mathbf{p}$来描述:
\[\mathbf{p} = [0, x, y, z]\] \[\mathbf{n}=[ n_x, n_y, n_z ]^T\] \[\mathbf{q} = [\cos \frac{\theta}{2}, \mathbf{n} \sin \frac{\theta}{2} ].\]四元数的共轭为:
\[\mathbf{q}^* = s - xi - yj - zk = [s, -\mathbf{v}]\]四元数的模长定义为:
\[\| \mathbf{q} \| = \sqrt{ s^2 + x^2 + y^2 + z^2 }\]四元数的逆为:
\[\mathbf{q}^{-1} = \mathbf{q}^* / \| \mathbf{q} \| ^2\]四元数$\mathbf{q}_a$和$\mathbf{q}_b$的乘为:
\[\begin{array}{lll} \mathbf{q}_a \mathbf{q}_b & = & s_a s_b - x_ax_b - y_ay_b - z_az_b \\ && + ( s_ax_b + x_as_b + y_az_b - z_ay_b )i \\ &&+ ( s_ay_b - x_az_b + y_as_b + z_ab_b )j \\ &&+ ( s_az_b + x_ay_b - x_by_a + z_as_b )k \end{array}\]旋转后的点$\mathbf{p}’$即可表示为这样的乘积
\[\mathbf{p}' = \mathbf{q} \mathbf{p} \mathbf{q}^{-1}\]$\mathbf{p}’$的虚部即为转换后的坐标点$[x’,y’,z’]$
Octave 下四元数计算点$[1, 1, 1]$绕$[-1, -1, 1]$
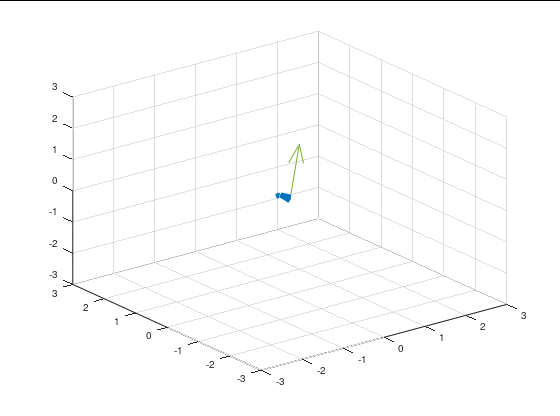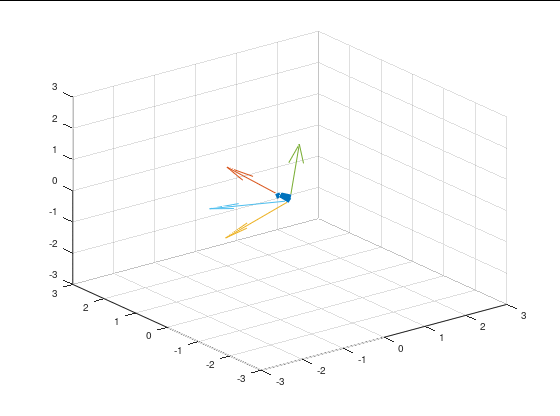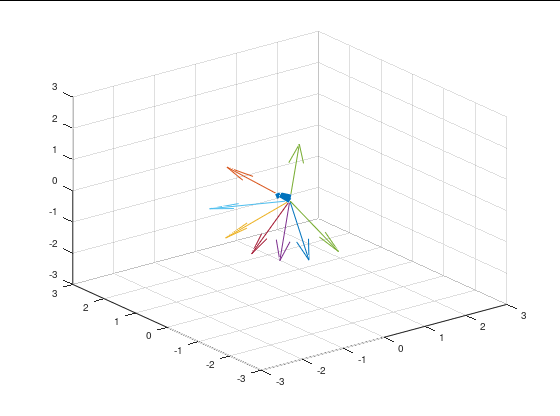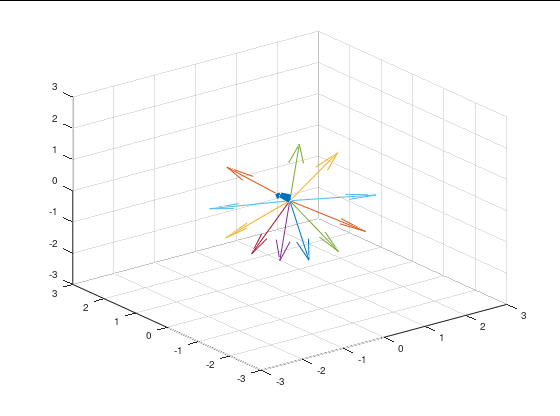
function dst = quaternion_rotate(src,axis,theta)
% lous quaternion_rotate - rotate a 3-D point src
% around axis theta radian
%
% Syntax: dst = quaternion_rotate(src,axis,theta)
%
pkg load quaternion
theta=theta/2;
p_src=quaternion (0,src(1),src(2),src(3));
q=quaternion(cos(theta),sin(theta)*axis(1),sin(theta)*axis(2),sin(theta)*axis(3));
qinv = inv (q);
p_dst=(q.*p_src).*qinv;
dst=[p_dst.x,p_dst.y,p_dst.z];
end