Lous Blog
相机标定
14 Jun 2019因相机检测到的位置在二维像坐标系下,而在大多数融合算法中我们都是用的全局坐标系。
相机标定方法
常见的标定方法有 直接线性变换法(DLT)、张正友标定
DLT
直接线性变换法
![]()
像素平面与像平面
物理坐标$(x_0,y_0)$对应像素坐标$(u_0,v_0)$
\[u = \frac{x}{dx}+u_0\] \[v = \frac{y}{dy}+v_0\]$dx$为在$x$方向上每个像素的宽度;$dy$为在$y$方向上每个像素的高度。
为何把转换矩阵从2X3填充至3X3?
\[\begin{bmatrix}u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx} & 0 & u_{0}\\ 0 & \frac{1}{dy} & v_{0}\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ 1\end{bmatrix}\]像平面与像空间
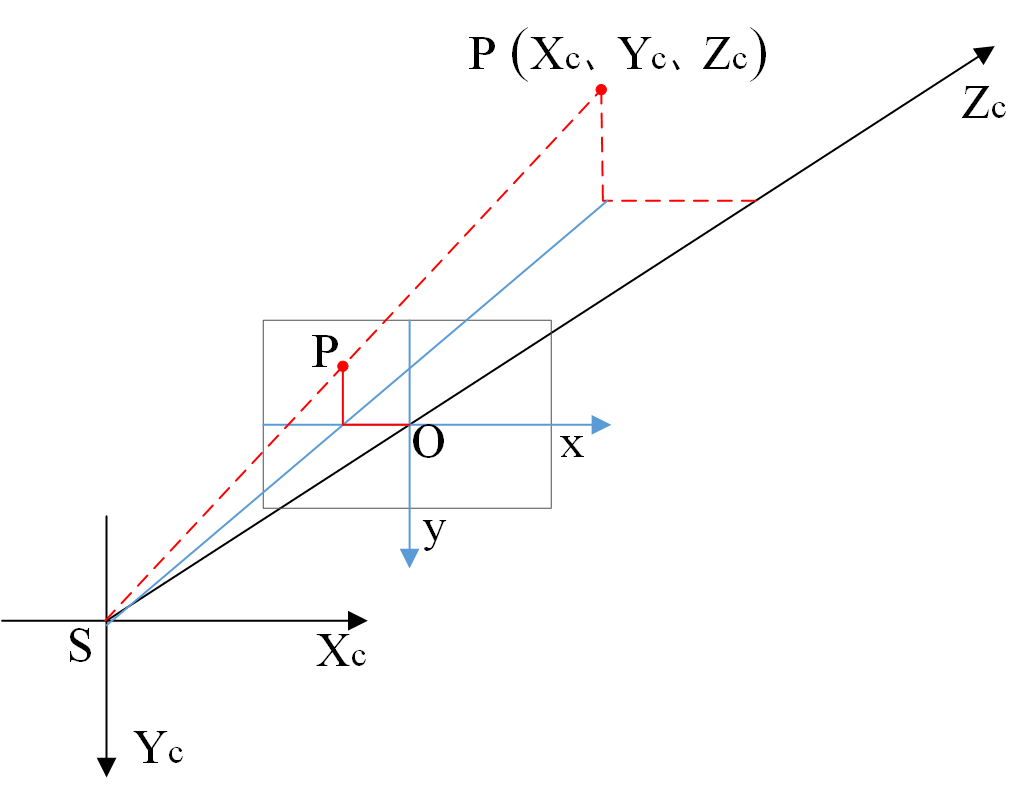
像空间坐标与全局坐标系
\[\begin{bmatrix}X_{C}\\ Y_{C}\\ Z_{C}\end{bmatrix}=R\begin{bmatrix}X\\ Y\\ Z\end{bmatrix}+\begin{bmatrix}X_{S}\\ Y_{S}\\ Z_{S}\end{bmatrix}\] \[\begin{bmatrix}X_{C}\\ Y_{C}\\ Z_{C}\\1\end{bmatrix}=\begin{bmatrix}R & t\\ 0^{T} & 1\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}=T\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}\] \[R=\begin{bmatrix}r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33}\end{bmatrix}\] \[t=\begin{bmatrix}t_{1}\\ t_{2}\\ t_{3}\end{bmatrix}\]像空间和全局坐标系
\[Z_C \begin{bmatrix} u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx} & 0 & u_{0}\\ 0 & \frac{1}{dy} & v_{0}\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}R & t\\ 0^{T} & 1\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1\end{bmatrix}\] \[Z_C \begin{bmatrix} u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}l_{1} & l_{2} & l_{3} & l_{4}\\ l_{5} & l_{6} & l_{7} & l_{8}\\ l_{9} & l_{10} & l_{11}& l_{12}\end{bmatrix}\begin{bmatrix}X\\ Y\\ Z\\1 \end{bmatrix}\]其中
\[Z_{C}=l_{9}X+l_{10}Y+l_{11}Z+l_{12}\] \[u=(l_{1}X+l_{2}Y+l_{3}Z+l_{4})/Z_{C}\] \[v=(l_{5}X+l_{6}Y+l_{7}Z+l_{8})/Z_{C}\] \[u=\frac{l_{1}X+l_{2}Y+l_{3}Z+l_{4}}{l_{9}X+l_{10}Y+l_{11}Z+1}\] \[v=\frac{l_{5}X+l_{6}Y+l_{7}Z+l_{8}}{l_{9}X+l_{10}Y+l_{11}Z+1}\]其中$l_{1}$至$l_{12}$各值为:
\[\begin{matrix} l_{1} &=& \frac{f\cdot r_{11}}{dx}+u_{0}\cdot r_{31} \\ l_{2} &=& \frac{f\cdot r_{12}}{dx}+u_{0}\cdot r_{32} \\ l_{3} &=& \frac{f\cdot r_{13}}{dx}+u_{0}\cdot r_{33} \\ l_{4} &=& \frac{f\cdot t_{1}}{dx}+u_{0}\cdot t_{3} \\ l_{5} &=& \frac{f\cdot r_{21}}{dx}+v_{0}\cdot r_{31} \\ l_{6} &=& \frac{f\cdot r_{22}}{dx}+v_{0}\cdot r_{32} \\ l_{7} &=& \frac{f\cdot r_{23}}{dx}+v_{0}\cdot r_{33} \\ l_{8} &=&\frac{f\cdot t_{2}}{dx}+v_{0}\cdot t_{3} \\ l_{9} &=& r_{31} \\ l_{10}&=& r_{32} \\ l_{11}&= &r_{33} \\ l_{12}&=&t_{3} \\ \end{matrix}\]求解
\[\begin{bmatrix}X & 0 \\ Y &0 \\ Z &0 \\ 1 &0 \\ 0 & X \\ 0 & Y \\ 0 & Z \\ 0 &1 \\ -Xu & -Xv \\ -Yu & -Yv \\ -Zu & -Zv \end{bmatrix}^T \begin{bmatrix} l_{1} \\ l_{2} \\ l_{3} \\ l_{4} \\ l_{5} \\ l_{6} \\ l_{7} \\ l_{8} \\ l_{9} \\ l_{10} \\ l_{11} \end{bmatrix}-\begin{bmatrix} u \\ v \end{bmatrix} = 0 \Rightarrow BL=C\] \[L = (B^T B)^{-1} (B^T C)\]内参数计算 通过旋转矩阵的特性可求得相机的内参数
\[\begin{matrix}u_{0}=l_{1}l_{9}+l_{2}l_{10}+l_{3}l_{11} \\ v_{0}=l_{5}l_{9}+l_{6}l_{10}+l_{7}l_{11} \\ f_{u}=\sqrt{l_{1}^{2}+l_{2}^{2}+l_{3}^{2}-u_{0}^{2}} \\ f_{v}=\sqrt{l_{5}^{2}+l_{6}^{2}+l_{7}^{2}-v_{0}^{2}}\end{matrix}\]张正友标定
暂无