Lous Blog
滤波器
04 Jun 2019数字滤波器
滤波器
FIR(Finite Impulse Response)滤波器:有限长单位冲激响应滤波器 IIR()
一阶滤波器
二阶滤波器
卡尔曼滤波器
过程
假设状态向量为$x \in \mathcal{R}^n$则$k$时刻的状态可由$k-1$时刻的状态表示如下:
\[x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\]$u \in \mathcal{R}^l $为系统输入,$w_k$为$k$时刻的过程噪声。
$A_{n \times n}$ 状态转移矩阵
$B_{n \times l}$ 控制输入矩阵
因为测量存在误差,假设$x$的观测值$z \in \mathcal{R}^m $:
\[z_k=Hx_k+v_k\]$H_{m \times n}$ 状态观测矩阵
$v_k$为$k$时刻的测量噪声。
假设$v$和$w$都为白噪声。
\[p(w) \sim N(0,Q)\] \[p(v) \sim N(0,R)\]计算
先验估计(预测)误差
\[e_k^- \equiv x_k - \hat{x} _k^-\]后验估计(测量)误差
\[e_k \equiv x_k - \hat{x} _k\]$\hat{x} _k^-$为$x_k$的先验值(观测值未获取时的预测值),$\hat{x} _k$为$x_k$的后验值(观测值$z_k$获取到后的估计值)。
\[e_{k+1}^- = x_{k+1} - \hat{x}_{k+1}^- \\ = (A x_k + B u_k + w_k) - (A \hat{x}_k + B u_k) \\ = A(x_k - \hat{x}_k) + w_k\]估计误差的协方差$P_k^-=E[ e_k^- e_k^{-T}]$
后验估计误差的协方差$P_k=E[ e_k e_k^T]$
我们可以通过一个权重系数$K \in [0,1] $来决定如何更新$x_k$的估计值,如果我们完全相信预测值$z_k$,$K=0$, $\hat{x}_k=\hat{x}_k^-$;如果我们完全相信测量值$\hat{x}_k = z_k$,$K=1$。
\[\hat{x}_k=\hat{x}_k^- + K(z_k - \hat{z}_k) \\ =\hat{x}_k^- + K(z_k - H \hat{x}_k^-) \\ =\hat{x}_k^- + K(H x_k + v_k - H \hat{x}_k^-) \\ =\hat{x}_k^- + KH x_k + K v_k - KH \hat{x}_k^-\]则有
\[e_k = x_k - \hat{x}_k \\ = x_k - ( \hat{x}_k^- + KH x_k + K v_k - KH \hat{x}_k^- ) \\ = (I-KH)(x_k - \hat{x}_k^-) - Kv_k \\ = (I-KH)e_k^- - K v_k\] \[P_k = E[e_ke_k^T] \\ = (I-KH) e_k^- (I-KH)^T - K R K^T \\ = P_k^- - KHP_k^- - P_k^- H^T K^T + K(H P_k^- H^T + R)K^T\]最优估计即使$P_k$最小
对$K$求偏导
\[\frac{\Theta P_k}{\Theta K} = -2(HP_k^-)^T + 2K(HP_K^-H^T +R )\]令$\frac{\Theta P_k}{\Theta K} = 0$,则有
\[K = P_k^- H^T (H P_k^- H^T + R)^{-1} \\ =\frac{P_k^-H^T}{H P_k^- H^T + R}\]$P_k^- = E[e_k^- e_k^{-T}]$ 代表先验误差的协方差
\[K = \frac{预测误差}{预测误差 + 测量误差}\]当测量值权重增大时,$R \downarrow K_k \uparrow $
当预测值权重增大时,$R \uparrow K_k \downarrow $
概率
\[E[x_k] = \hat{x}_k\] \[P_k = E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T]\] \[P_{k+1}^- = E[ e_{k+1}^- e_{k+1}^{-T}] \\ = E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T] \\ =E[(Ae_k+w_k)(Ae_k+w_k)^T] \\ =E[(Ae_k)(Ae_k)^T] + E[w_kw_k^T] =A E[e_ke_k^T] A^T + Q \\ =A P_k A^T + Q\]说明下次的预测误差$P_k^-$由本次的估计误差$P_k$和过程误差$Q$组成
卡尔曼滤波器的计算过程
for(;;)
{
time_update();
measurement_update();
}
预测阶段
\[\hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}\] \[P_k^- = A P_{k-1} A^T + Q\]估计阶段
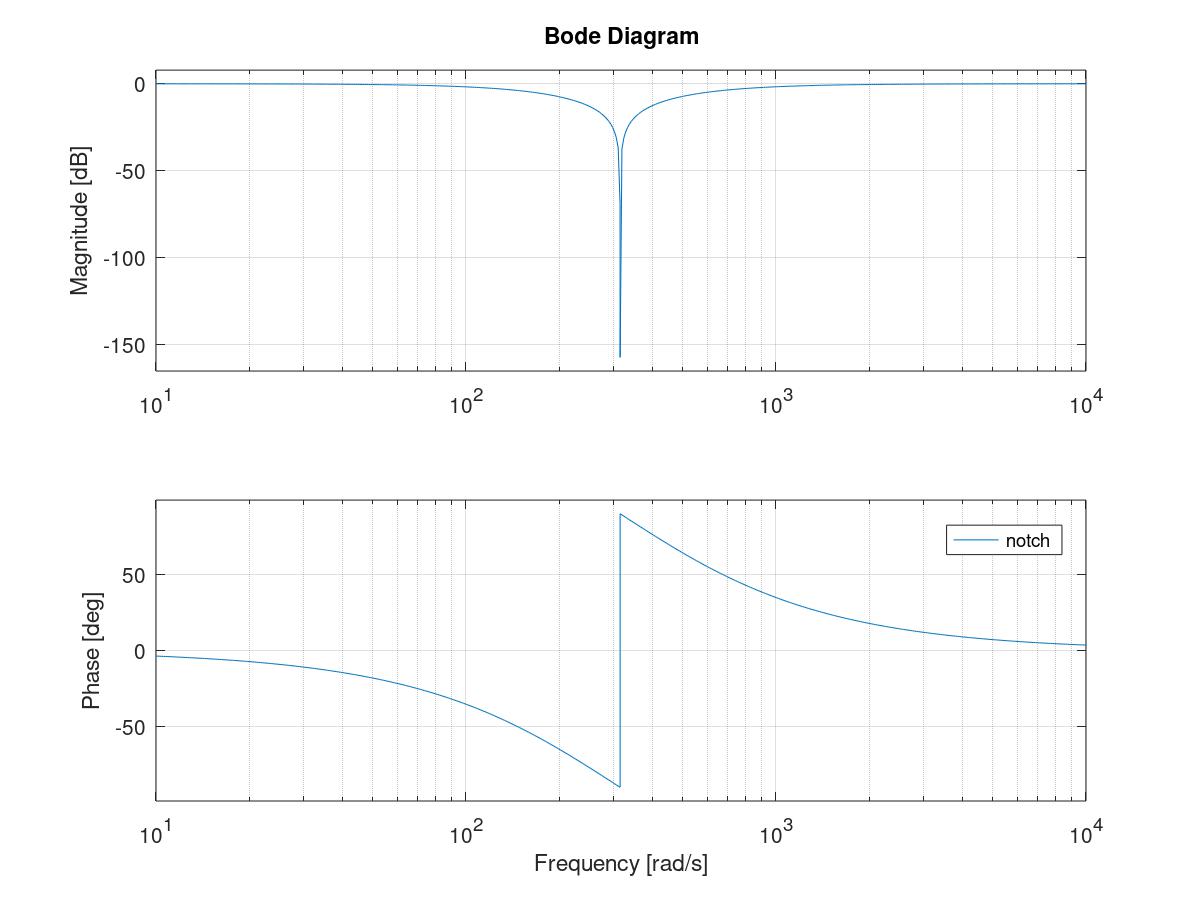
\[K_k = P_k^- H^T (H P_k^- H^T + R)^{-1}\] \[P_k = (I - K_kH)P_k^-\] \[\hat{x}_k = \hat{x}_k^- + K_k (z_k - H \hat{x}_k^-)\]陷波滤波器 (notch filter)
理想情况下陷波滤波器是个点阻滤波器,实际工程上是一个非常窄的带阻滤波器。
滤波器传递函数
\[G(s)=\frac{s^2+\omega_n^2}{s^2+2\omega_ns+\omega_n^2}\]其Bode图如下