Lous Blog
Setpoint
03 May 2019设置生成点
作用
预先设置被控对象需要到达的状态,和过程中的每一个状态。
轨迹规划
多自由度机械手
单轴轨迹规划
补充某场景下仿真,例如一质量为1kg的木块,在桌面上的静摩擦力系数为Ks,动摩擦力系数为Km,电机出力为线性的F=K·Input。设置点从0m以最大加速度1m/s^2,最大速度0.5m/s走到1m处。分析计算整个行程内的位置误差和速度误差。假设采样周期为1ms。
Octave 计算SPG图如下
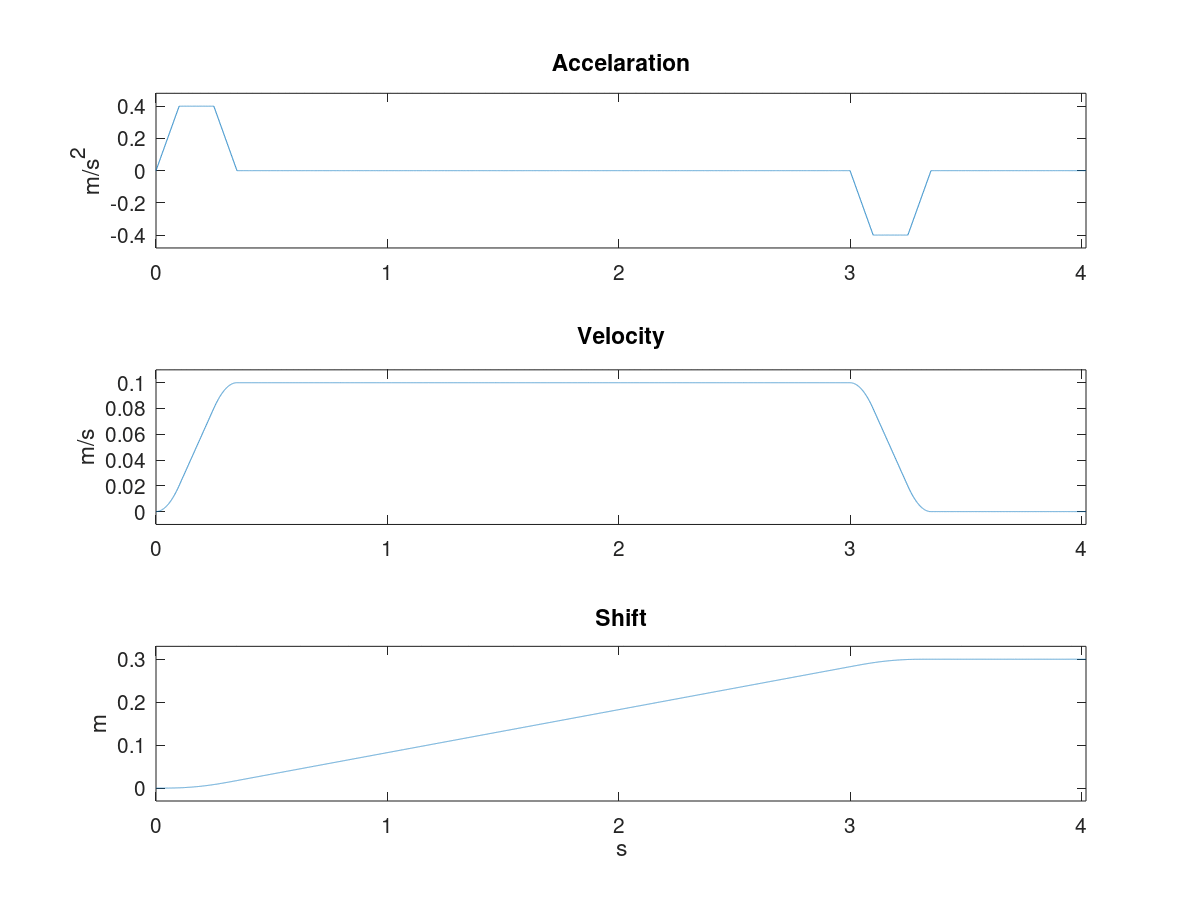
对于位置环我们可以提前规划位移s与时间t之间的关系s(t)。
从A点运动到B点,距离为$Dist$,最大加速度为$Acc$,最大速度为$Vel$。
假如在A点开始运动立马进入匀加速段,则在A点电机会有个很大的冲击力。 为了避免这个冲击,我们需要定义一个加加速度$Jerk$。
因此一共有个阶段
1.匀加加速度段 ($t_0$ ~ $t_1$) 2.匀加速段 ($t_1$ ~ $t_2$) 3.匀减减速段 ($t_2$ ~ $t_3$) 3.匀速段 ($t_3$ ~ $t_4$) 4.匀减减速段 ($t_4$ ~ $t_5$) 5.匀减速段 ($t_5$ ~ $t_6$) 6.匀加加速度 ($t_6$ ~ $t_7$)
匀加加速度段 ($t_0$ ~ $t_1$)
$t_0=0$时刻从A到B点首先是一个加加速段,
匀加加速段持续时间$t_{jerk}=\frac{Acc}{Jerk}$
结束时刻$t_1=t_0+\frac{Acc}{Jerk}$。
$t_0$~$t_1$内
加速度$a(t)=\int_0^tJerkdt
=Jerk{\cdot}t$.
速度$v(t)=\int_0^ta(t)dt
=\int_0^tJerk{\cdot}tdt
=\frac{Jerk{\cdot}t^2}{2}$.
位移$s(t)=\int_0^tv(t)dt
=\int_0^t\frac{Jerk{\cdot}t^2}{2}dt
=\frac{Jerk{\cdot}t^3}{6}$
则在结束匀加加速度时刻$t_1$
速度$v_1=\frac{Jerk\cdot{t_1}^2}{2}
=\frac{Jerk\times({\frac{Acc}{Jerk}})^2}{2}
=\frac{Acc^2}{2{\cdot}Jerk}$
位移$s_1=\frac{Jerk{\cdot}t_1^3}{6}=\frac{Acc^3}{6{\cdot}Jerk^2}$
移动距离 $d_1=|s_1|=\frac{Acc^3}{6{\cdot}Jerk^2}$
匀加速段 ($t_1$ ~ $t_2$)
$t_1$时刻到$t_2$
因为有匀减减速段的存在,所以速度不能直接在匀速的到达最大值。
$v_2=Vel-v_1
=Vel-\frac{Acc^2}{2{\cdot}Jerk}$
匀加速段持续时间$t_{acc}=\frac{v_2-v_1}{Acc}
=\frac{Vel-\frac{Acc^2}{Jerk}}{Acc}
=\frac{Vel}{Acc}-\frac{Acc}{Jerk}$
$t_2=t_1+t_{acc}=\frac{Vel}{Acc}$
加速度$a(t)=Acc$
速度\(v(t)=v_1+\int_{t_1}^{t}a(t)dt\\ =v_1+\int_{t_1}^{t}Accdt\\ =v_1+Acc\cdot(t-t_1)\\ =\frac{Acc^2}{2{\cdot}Jerk}+Acc\cdot(t-\frac{Acc}{Jerk})\\ =Acc{\cdot}{t}-\frac{Acc^2}{2{\cdot}Jerk}\).
位移\(s(t)=s_1+\int_{t_1}^tv(t)dt\\ =s_1+\int_{t_1}^t(Acc{\cdot}{t}-\frac{Acc^2}{2{\cdot}Jerk})dt\\ =s_1+\frac{Acc}{2}(t^2-t_1^2)-\frac{Acc^2}{2{\cdot}Jerk}{\cdot}(t-t_1)\\ =\frac{Acc}{2}{\cdot}t^2-\frac{Acc^2}{2{\cdot}Jerk}{\cdot}t+s_1-\frac{Acc}{2}{\cdot}t_1^2+\frac{Acc^2}{2{\cdot}Jerk}{\cdot}t_1\\ =\frac{Acc}{2}{\cdot}t^2-\frac{Acc^2}{2{\cdot}Jerk}{\cdot}t+\frac{Acc^3}{6{\cdot}Jerk^2}\)
$s_2=\frac{Vel^2}{2Acc}-\frac{Vel{\cdot}Acc}{2{\cdot}Jerk}+\frac{Acc^3}{6{\cdot}Jerk^2}$
匀减减速段 ($t_2$ ~ $t_3$)
持续时间也为$t_{jerk}=\frac{Acc}{Jerk}$
$t_3=t_2+t_{jerk}
=\frac{Vel}{Acc}+\frac{Acc}{Jerk}$
$a(t)=Acc-Jerk{\cdot}(t-\frac{Vel}{Acc})$
\[v(t)=v_2+\int_{t_2}^{t}a(t)dt\\ =v_2+(Acc+\frac{Jerk{\cdot}Vel}{Acc})(t-t_2)-\frac{Jerk}{2}(t^2-t_2^2)\\ =-\frac{Jerk}{2}{\cdot}t^2+(Acc+\frac{Jerk{\cdot}Vel}{Acc}){\cdot}t-\frac{Acc^2}{2{\cdot}Jerk}-\frac{Jerk{\cdot}Vel^2}{2{\cdot}Acc^2}\] \[s(t)=s_2+\int_{t2}^tv(t)dt\\ =-\frac{Jerk}{6}{\cdot}t^3+\frac{Acc+\frac{Jerk{\cdot}Vel}{Acc}}{2}{\cdot}t^2-\frac{1}{2}(\frac{Acc}{Jerk}+\frac{Jerk{\cdot}Vel^2}{Acc})t-\frac{Jerk{\cdot}Vel^3}{3Acc^3}-\frac{Vel^2}{2Acc}+\frac{Acc{\cdot}Vel}{2Jerk}+\frac{Jerk{\cdot}Vel^2}{2Acc^2}\]$a_3=0$,$v_3=Vel$ $v_3=Vel$ $s_3=\frac{1}{2}{\cdot(\frac{Vel{\cdot}Acc}{Jerk}+\frac{Vel^2}{Acc})}$
匀速段 ($t_3$ ~ $t_4$)
\[t_{vel}=\frac{Dist-2s_3}{Vel}\\ =\frac{Dist}{Vel}-\frac{Vel}{Acc}-\frac{Acc}{Jerk}\]$t_4=\frac{Dist}{Vel}$
$a(t)=0$
$v(t)=Vel$
\[s(t)=s_3+Vel(t-t_3)\\ =Vel{\cdot}t-\frac{Vel}{2}(\frac{Vel}{Acc}+\frac{Acc}{Jerk})\]$s_4=Dist-\frac{Vel}{2}(\frac{Vel}{Acc}+\frac{Acc}{Jerk})$
$v_4=v_3=Vel$
匀减减速段 ($t_4$ ~ $t_5$)
\[t_{jerk}=\frac{Acc}{Jerk}\] \[t_5=\frac{Dist}{Vel}+\frac{Acc}{Jerk}\] \[a(t)=-Jerk(t-t_4)\\ =-Jerk{\cdot}t+\frac{Jerk{\cdot}Dist}{Vel}\] \[v(t)=v_4+\int_{t_4}^{t}a(t)dt\\ =-\frac{Jerk}{2}t^2+\frac{Jerk{\cdot}Dist}{Vel}t+Vel-\frac{Jerk{\cdot}Dist^2}{2Vel^2}\]$v_5=v_2=Vel-\frac{Acc^2}{2{\cdot}Jerk}$
$a_5=-Acc$
$$
匀减速段 ($t_5$ ~ $t_6$)
$t_{acc}=\frac{Vel}{Acc}-\frac{Acc}{Jerk}$
$a(t)=-Acc$
$v(t)=v_5+\int_{t_5}^ta(t)dt
=Vel-\frac{Acc^2}{2{\cdot}Jerk}-Acc(t-t_5)
=-Acc{\cdot}t+Vel+\frac{Acc^2}{2Jerk}+\frac{Acc{\cdot}Dist}{Vel}$
$s(t)=s_5+\int_{t_5}^tv(t)dt$
$t_6=\frac{Dist}{Vel}+\frac{Vel}{Acc}$
$a_6=-Acc$
$v_6=v_1=\frac{Acc^2}{2{\cdot}Jerk}$
$s_6=$
匀加加速度 ($t_6$ ~ $t_7$)
$t_{jerk}=\frac{Acc}{Jerk}$
$t_7=\frac{Vel}{Acc}+\frac{Vel}{Acc}+\frac{Acc}{Jerk}$
$a(t)=-Acc+Jerk(t-t_6)
=Jerk{\cdot}t-Acc+Jerk(\frac{Dist}{Vel}+\frac{Vel}{Acc})$
$a_7=0$
$v_7=0$
$s_7=Dist$