Lous Blog
Octave 卡尔曼滤波器仿真
16 Jun 2019多传感器信息融合中经常会使用到卡尔曼滤波器。
具体推导过程请参见滤波器
迭代过程
预测阶段
\[\hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}\] \[P_k^- = A P_{k-1} A^T + Q\]估计阶段
\[K_k = P_k^- H^T (H P_k^- H^T + R)^{-1}\] \[P_k = (I - K_kH)P_k^-\] \[\hat{x}_k = \hat{x}_k^- + K_k (z_k - H \hat{x}_k^-)\]测试数据
数据从Arduino 超声波模块获取到一组测量数据
测试时传感器和被测物体并未发生相对位移,故理想距离应该不变。
测试脚本
clear ;close all; clc;
load 'sonar.txt'
R=std(sonar);%测量噪声
Q=std(sonar);%过程噪声
A=1;
B=1;
H=1;
z=sonar(1:400);%观测值
u=zeros(size(z));%输入值
K=zeros(size(z));%卡尔曼增益
t=1:length(z);
Q=0.01*std(sonar);%过程噪声
[x,K]=kalman_filter(z,u,A,B,R,Q,H);
figure(1)
filename = 'kalman_filter_R_change.gif';
for i=1:10
Q=std(sonar);%过程噪声
R=std(sonar)*i;
[x,K]=kalman_filter(z,u,A,B,R,Q,H);
plot(t,z,t,x);
legend('measurement','kalman filtered')
title(['Q=' ,num2str(Q),' R=',num2str(R)])
drawnow
frame = getframe(1);
im = frame2im(frame);
[imind,cm] = rgb2ind(im);
if i == 1;
imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',1);
else
imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',1);
end
end
close all;
figure(1)
filename = 'kalman_filter_Q_change.gif';
for i=1:10
R=std(sonar);%测量噪声
Q=std(sonar)/i;
[x,K]=kalman_filter(z,u,A,B,R,Q,H);
plot(t,z,t,x);
legend('measurement','kalman filtered')
title(['Q=' ,num2str(Q),' R=',num2str(R)])
drawnow
frame = getframe(1);
im = frame2im(frame);
[imind,cm] = rgb2ind(im);
if i == 1;
imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',1);
else
imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',1);
end
end
close all;
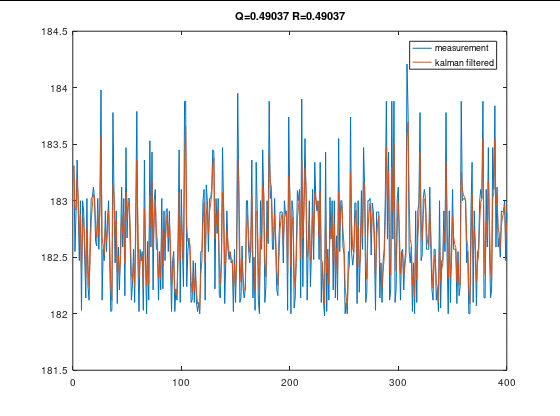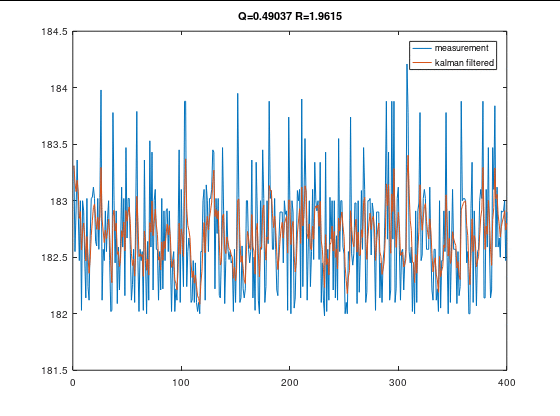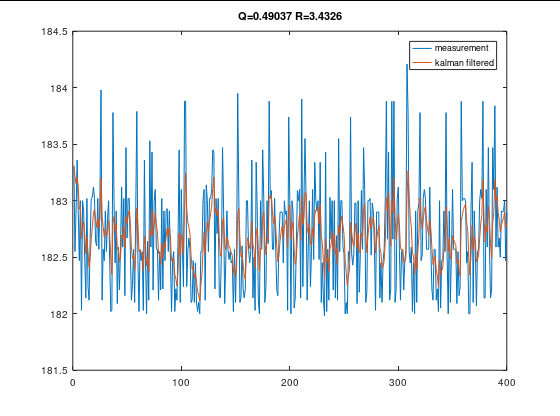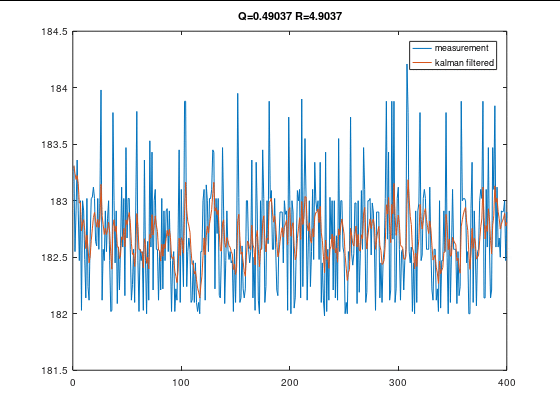
Q R 值对滤波效果的影响
R不变时,Q变小
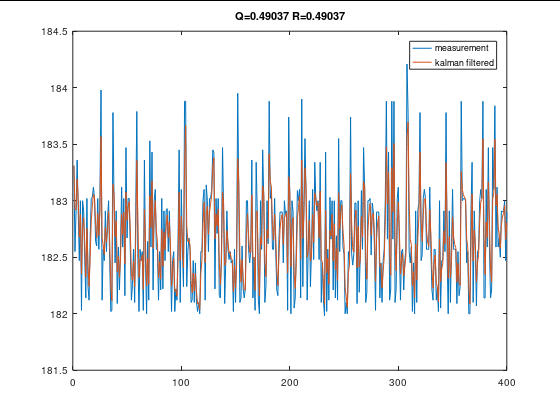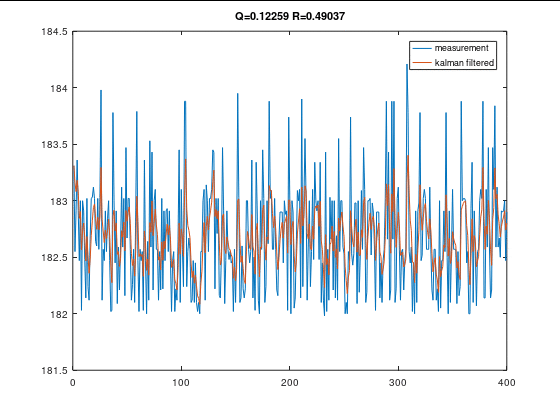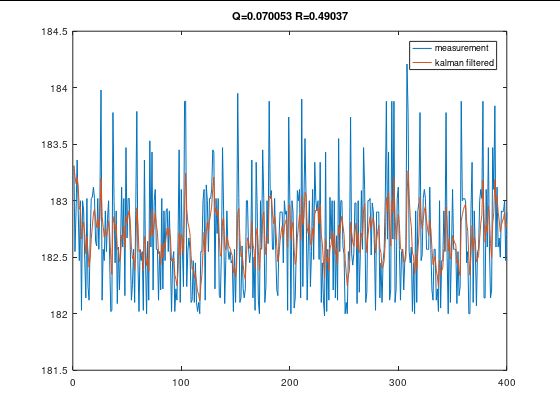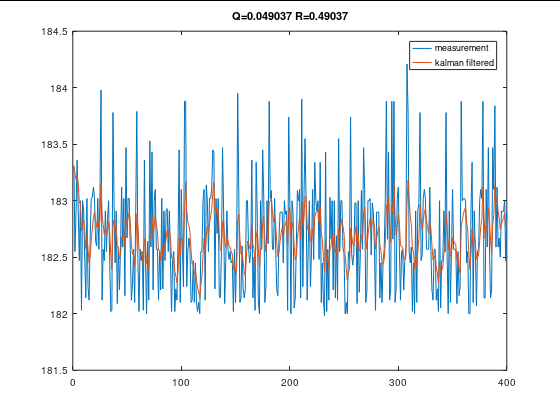
Q不变时,R变大